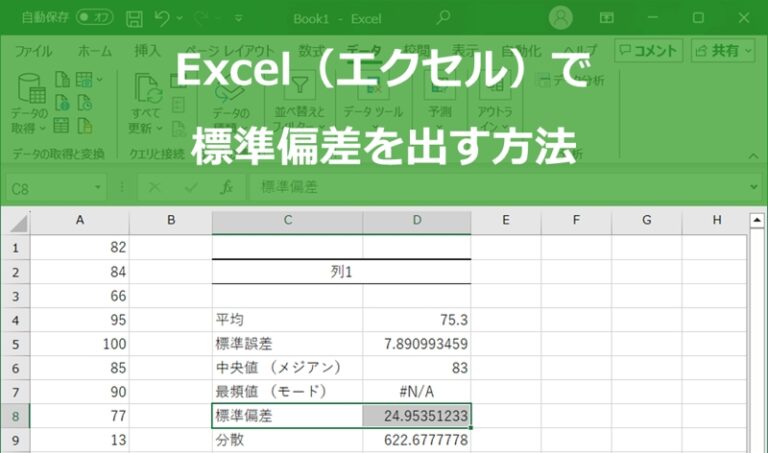
Excel(エクセル)は、データ分析や統計計算において非常に強力なツールです。その中でも、標準偏差はデータのばらつきを評価するためによく使用される統計指標です。
本記事では、Excel(エクセル)で標準偏差を計算する方法について、具体的なステップと実践的なテクニックを詳しく解説します。この記事を読むことで、Excel(エクセル)の標準偏差計算に関する基本的な知識から、実際の業務で役立つ応用テクニックまでをマスターできるでしょう。
関数を活用したり、適切なグラフを作成して視覚的にわかりやすい資料に変換したりすることで、Excel(エクセル)を用いたデータ分析をさらに深め、実務に直結するスキルを身につけましょう。
標準偏差とは

標準偏差とは、データセット内の各データポイントが平均値からどれだけ離れているかを示す統計的な指標です。具体的には、データの散らばり具合やばらつきの度合いを数値化したものであり、分散の平方根として計算されます。
標準偏差が小さい場合、データポイントは平均値に近い値に集中していることを示し、逆に標準偏差が大きい場合、データポイントは平均値から遠く離れていることを示します。これにより、データの分布や変動の特徴を把握するのに役立ちます。
標準偏差の計算方法
標準偏差を計算するための基本的なステップは以下の通りです。
- データセットの平均値を計算する: まず、データセット中のすべての値の合計を求め、その総和をデータポイントの数で割ります。これが平均値(μ)です。例えば、データセットが[10, 12, 23, 23, 16, 23, 21, 16]である場合、まず平均値を計算します。この場合、データセットの数を全て足した144にデータの個数である8で割って平均値は18になります。
- 偏差を求める: 偏差とは、データセットのそれぞれの値から平均値を引いた数値のことです。今回の例の場合は23-18=5、10-18=-8などが偏差です。
- 偏差の二乗を計算する: 各偏差を二乗し、全ての二乗値を合計します。このステップは、正負の差をすべて正の値に変換するために行います。各偏差の二乗の合計は192です。
- 分散を求める: 二乗値の合計をデータポイントの数で割ります。これにより、分散(σ²)が得られます。分散は192÷8=24
- 標準偏差を出す: 最後に、分散の平方根を取ることで標準偏差(σ)が得られます。24の平方根は4.89です。
分散を計算する際、母集団全体を対象にする場合と、サンプルデータを対象にする場合で計算方法が若干異なります。母集団全体の場合はデータの数で割りますが、サンプルの場合はデータの数から1を引いた値で割ります。これにより、サンプルのバイアスを補正することができます。
標準偏差の計算は、データのばらつきを理解するために非常に重要です。特に、データの変動が大きい場合や異常値が含まれている場合に、その影響を評価するために役立ちます。標準偏差が小さい場合、データポイントは平均値の周りに密集しており、一貫性があることを示します。逆に、標準偏差が大きい場合、データポイントは広範囲に分散しており、変動が大きいことを示します。
Excel(エクセル)で標準偏差を計算する方法

Excel(エクセル)は、データ分析に欠かせないツールであり、標準偏差を計算するための関数や機能が豊富に揃っています。この記事では、Excel(エクセル)を用いて標準偏差を計算する基本的な方法について説明します。
まず、データセットを準備し、Excel(エクセル)の関数を利用して標準偏差を求める手順を確認しましょう。Excel(エクセル)には、標本標準偏差を計算するためのSTDEV.S関数と、母集団標準偏差を計算するためのSTDEV.P関数があります。さらに、データ分析ツールを使用して標準偏差を求める方法も解説します。
STDEV.S関数を使った標準偏差の出し方
STDEV.S関数は、Excel(エクセル)で標本標準偏差を計算するために使用されます。標本標準偏差とは、データセット内の各データが平均からどれくらい離れているかを表す指標です。分散の平方根を取ったもので、データの散らばり具合を測るために使われます。
標本標準偏差は、データセットが全体の一部である場合に適用されます。STDEV.S関数の使い方は非常に簡単です。まず、標準偏差を計算したいデータが含まれているセル範囲を選択し、その範囲を関数の引数として入力します。
例えば、セルA1からA10までのデータの標本標準偏差を求める場合、関数は次のようになります:=STDEV.S(A1:A10)。
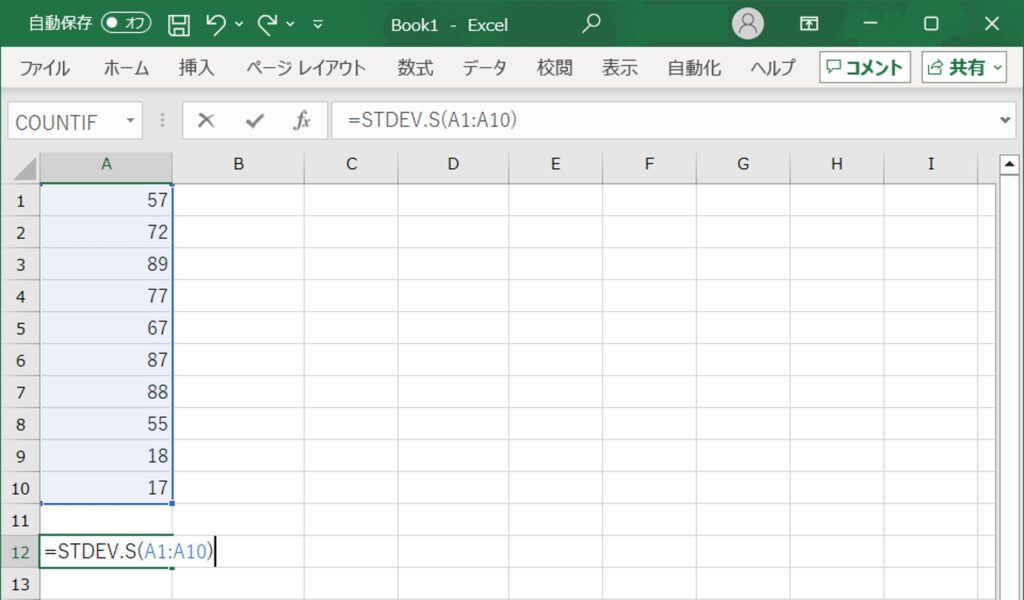
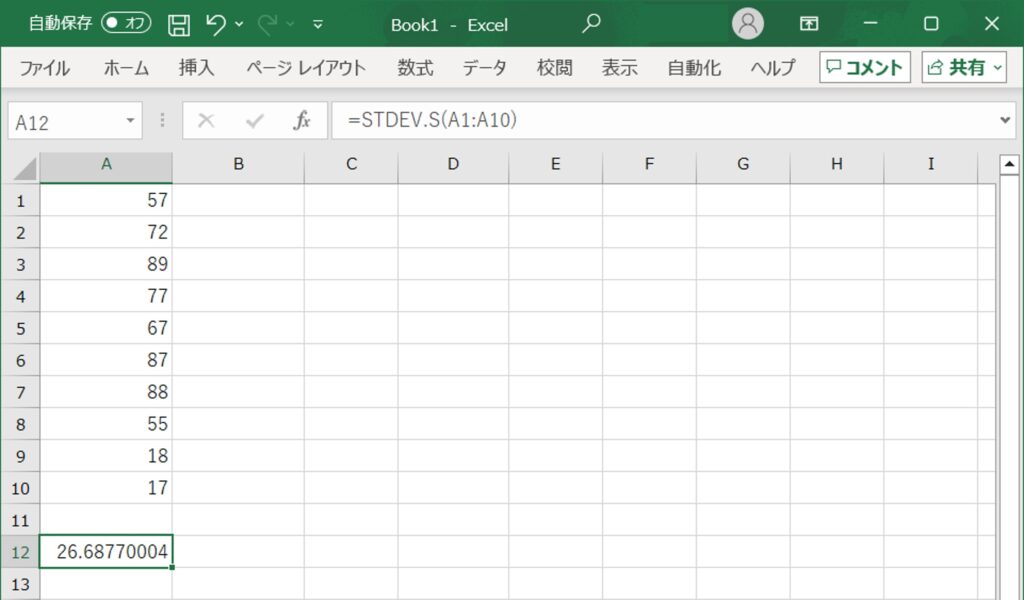
この関数を入力してEnterキーを押すと、選択したデータ範囲の標本標準偏差が計算され、セルに表示されます。
STDEV.P関数を使った標準偏差の出し方
STDEV.P関数は、Excel(エクセル)で母集団標準偏差を計算するために使用されます。母集団標準偏差とは、全てのデータ(母集団)の散らばり具合を測る指標です。データが平均値の周りにどの程度集まっているか、あるいは散らばっているかを示します。
母集団標準偏差は、データセットが全体の母集団を表す場合に適用されます。STDEV.P関数の使い方も簡単です。標準偏差を計算したいデータが含まれているセル範囲を選択し、その範囲を関数の引数として入力します。
例えば、セルA1からA10までのデータの母集団標準偏差を求める場合、関数は次のようになります:=STDEV.P(A1:A10)。
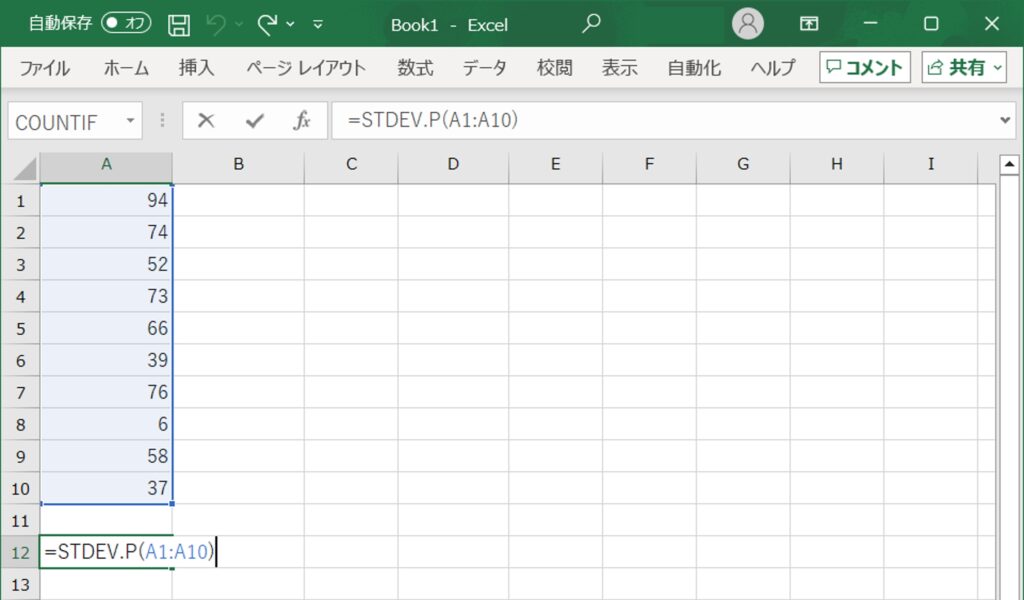
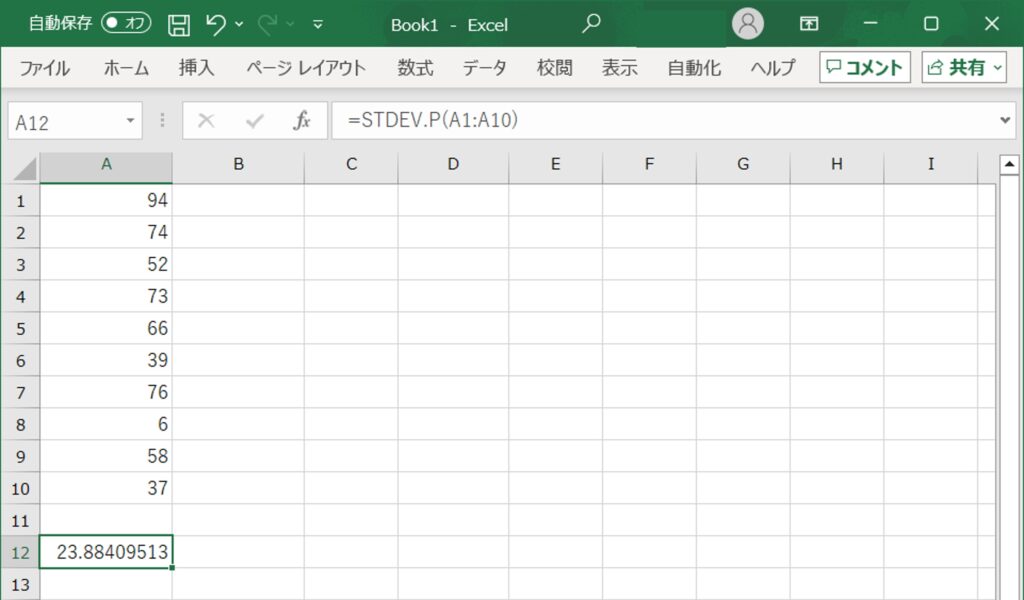
この関数を入力してEnterキーを押すと、選択したデータ範囲の母集団標準偏差が計算され、セルに表示されます。
データ分析ツールを使用して標準偏差を求める
Excel(エクセル)には、データ分析ツールという便利な機能があり、これを使用することでより詳細なデータ分析が可能です。データ分析ツールを使用するには、まず「データ」タブをクリックし、「データ分析」ボタンを選択します。次に表示される「データ分析」ダイアログボックスから「基本統計量」を選び、「OK」をクリックします。

続いて、標準偏差を計算したいデータ範囲を入力し、出力範囲を指定します。
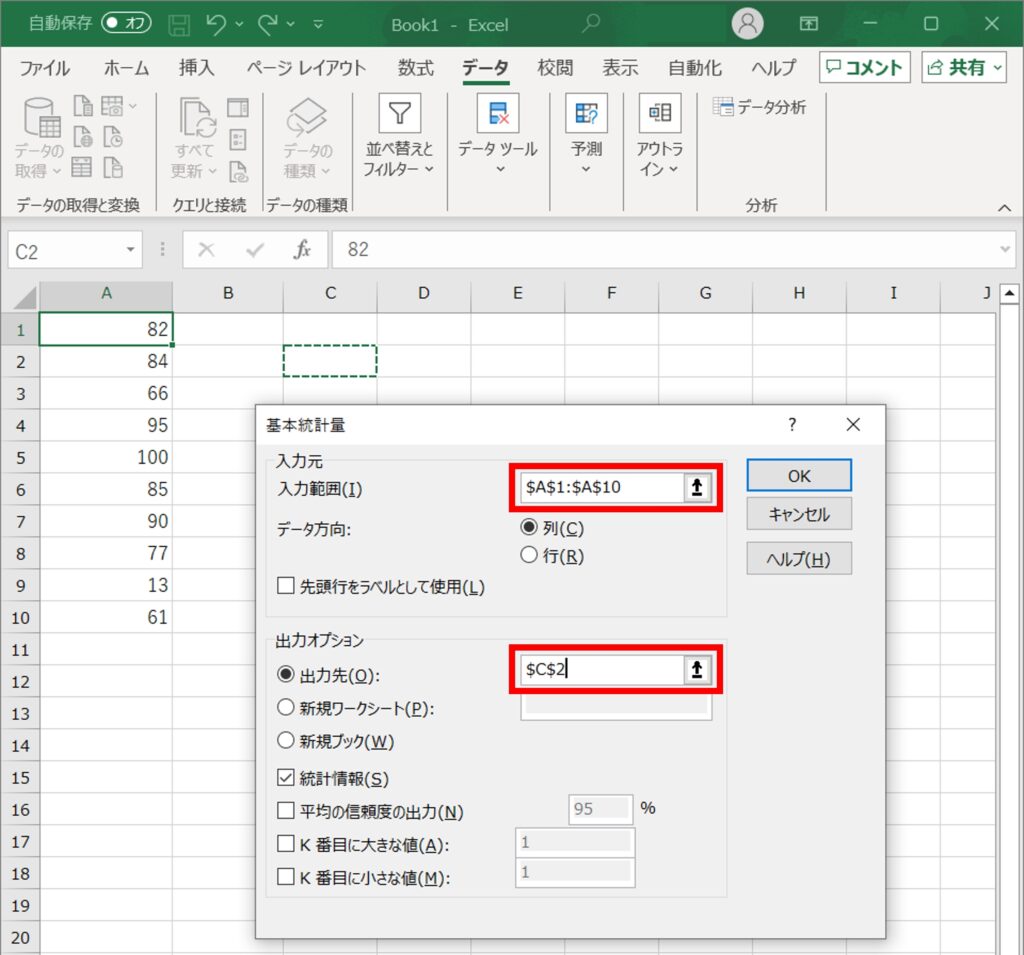
最後に「OK」をクリックすると、選択したデータの標準偏差を含む詳細な統計情報が表示されます。
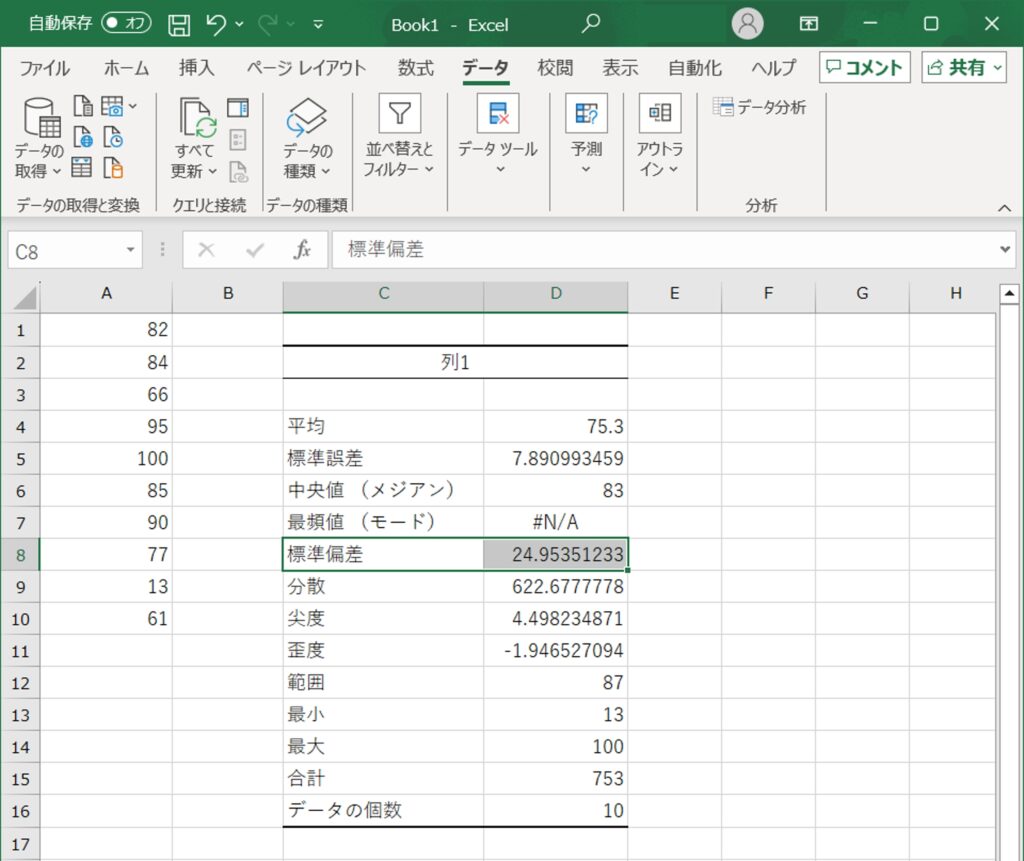
この方法は、大量のデータを扱う場合や、他の統計指標と一緒に標準偏差を確認したい場合に非常に有用です。
標準偏差をわかりやすいグラフに変換する方法
Excel(エクセル)で標準偏差を計算した後、その結果を視覚的に伝えるためには、適切なグラフに変換することが重要です。以下では、エラーバー付き棒グラフと散布図を用いて標準偏差をわかりやすく表現する方法について説明します。
エラーバー付き棒グラフに変換する
エラーバー付き棒グラフは、データの平均値とその変動範囲(標準偏差)を一目で理解できるため、非常に有用です。Excel(エクセル)でエラーバー付き棒グラフを作成する手順は以下の通りです。
- データの入力:まず、平均値と標準偏差のデータをExcel(エクセル)シートに入力します。例えば、各行に異なるカテゴリや条件のデータを入力します。
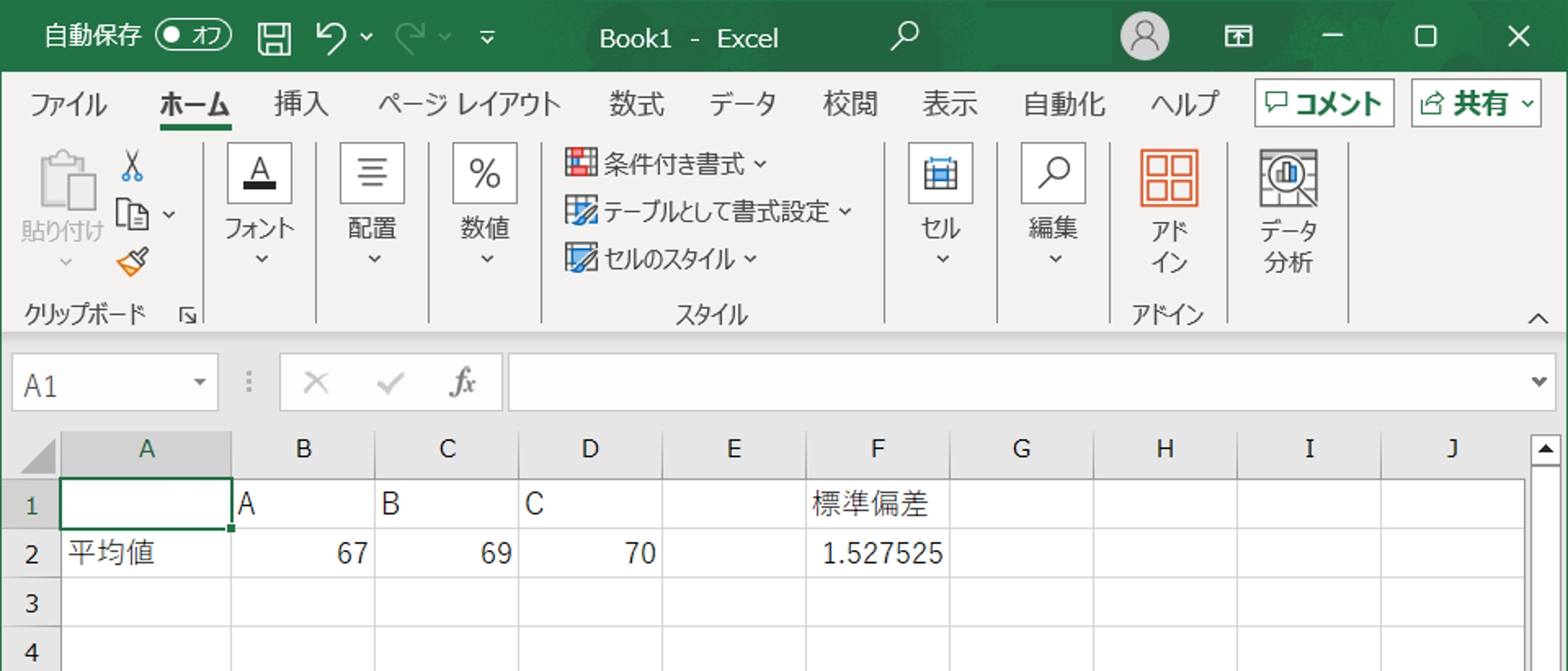
- グラフの作成:データ範囲を選択し、Excel(エクセル)のリボンから「挿入」タブをクリックします。「棒グラフ」を選択し、基本的な棒グラフを作成します。
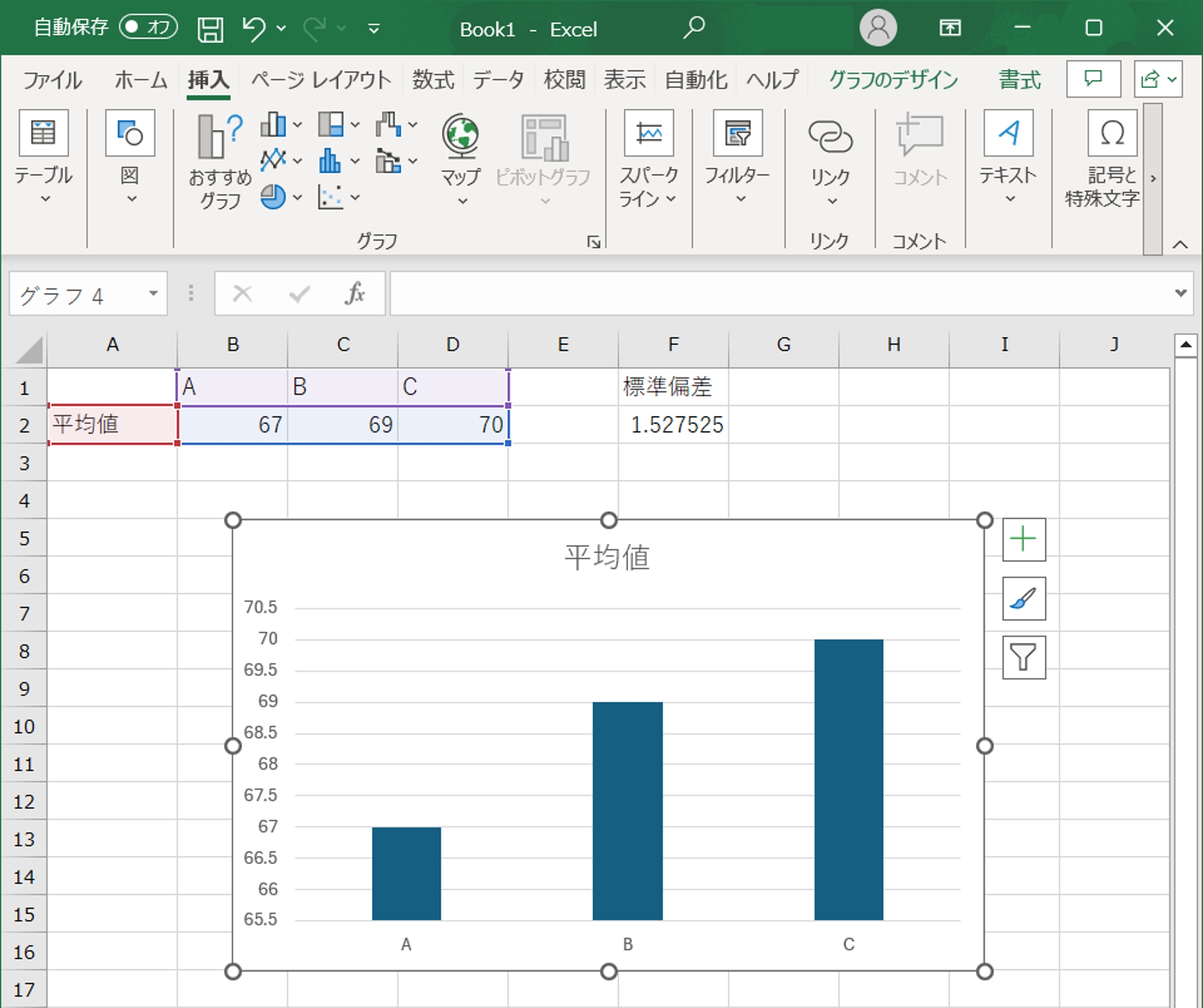
- エラーバーの追加:作成した棒グラフをクリックし、グラフツールの「デザイン」タブから「グラフ要素を追加」を選び、「誤差範囲」をクリックします。
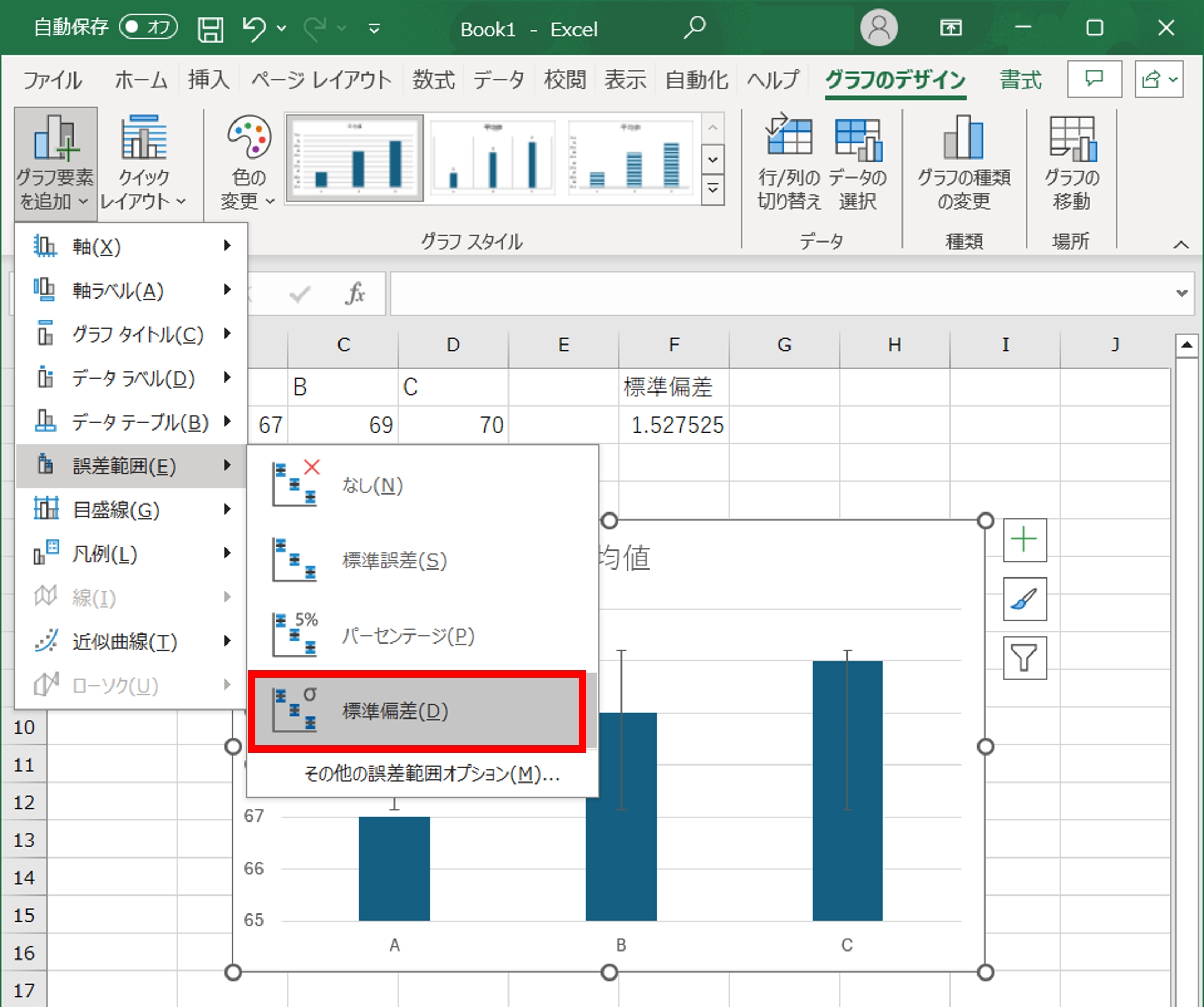
「標準偏差」を選択することで、自動的にエラーバーが追加されます。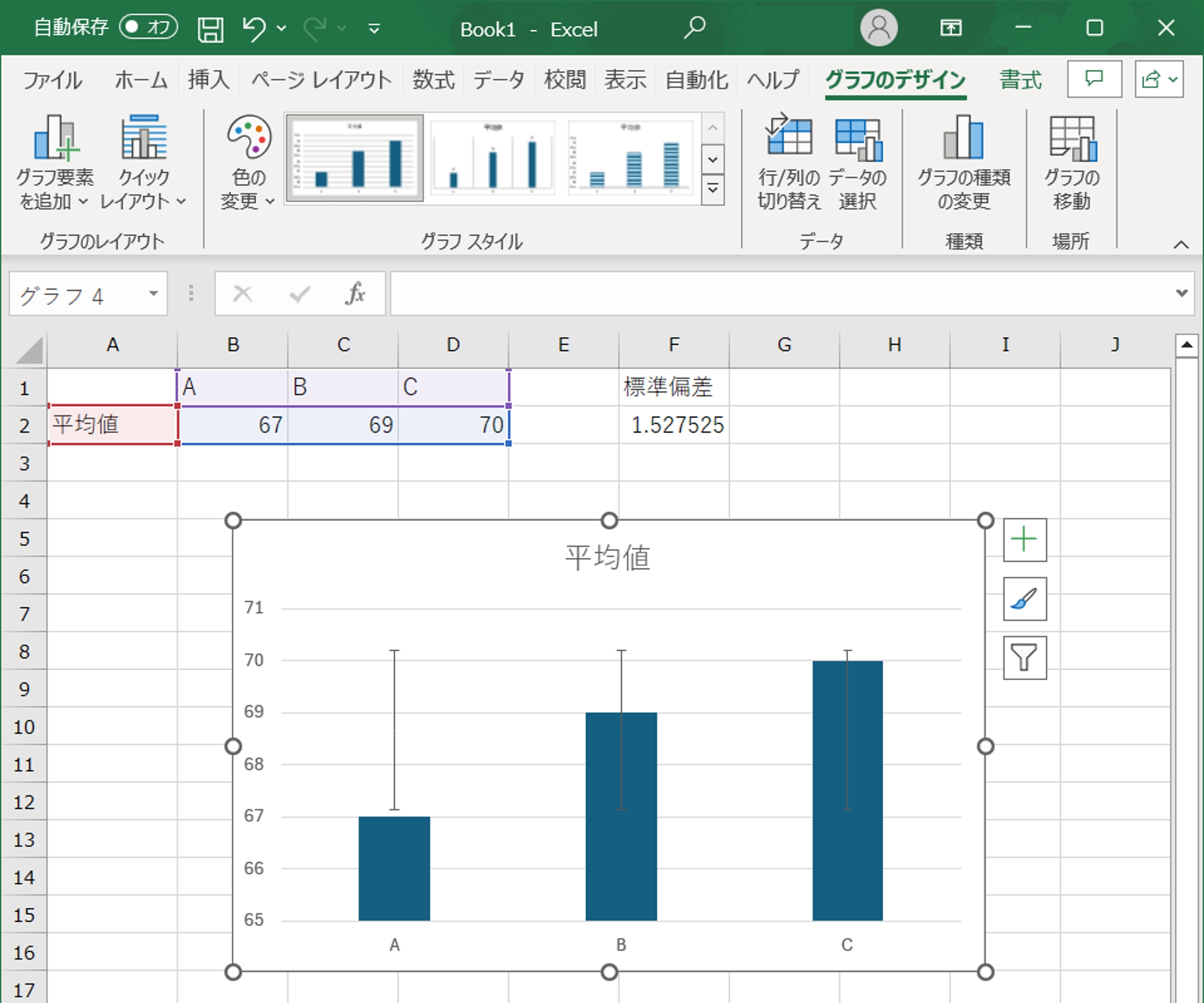
- エラーバーの編集:エラーバーの種類や表示形式をカスタマイズしたい場合、エラーバーを右クリックし、「誤差範囲の書式設定」を選びます。
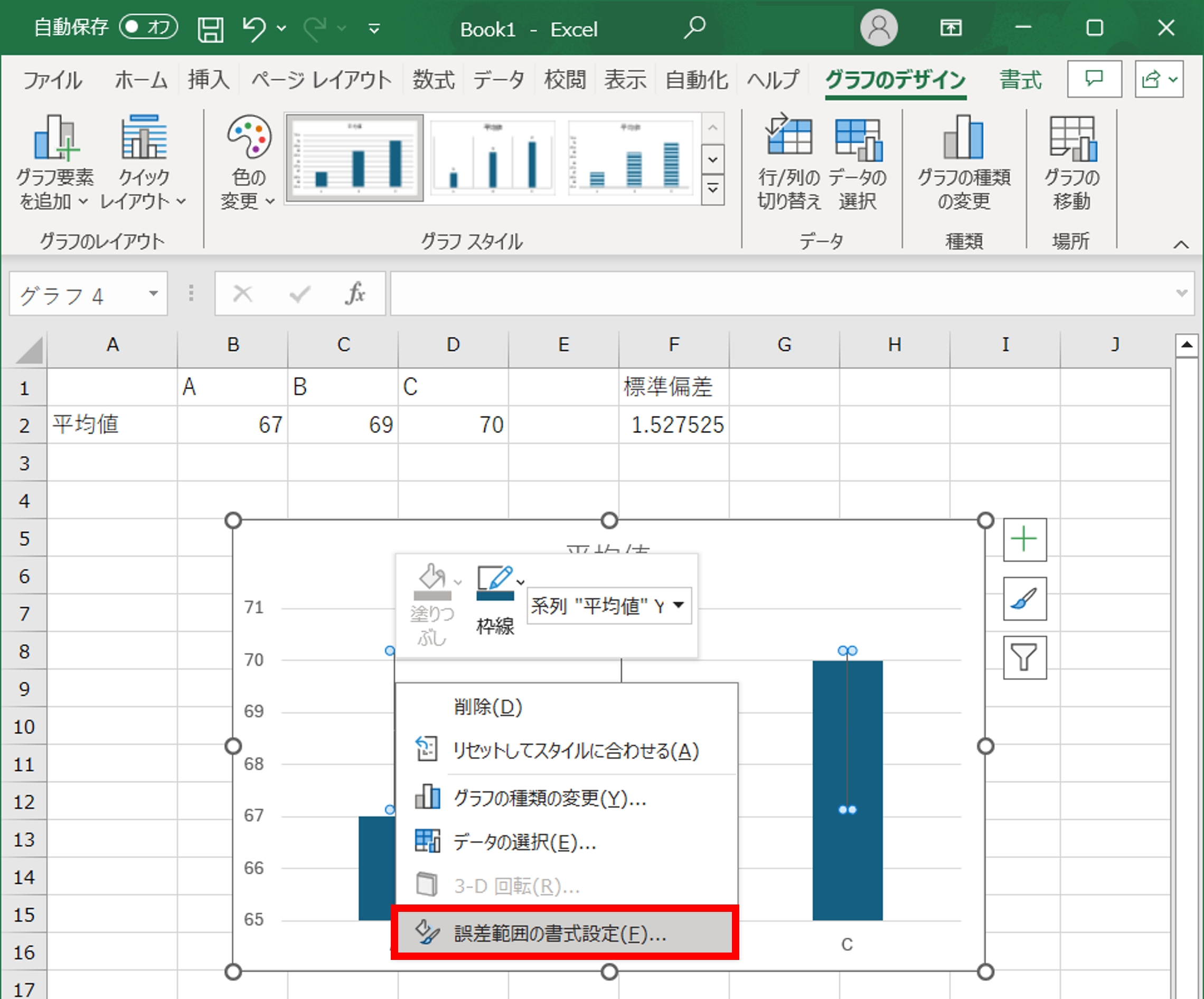
ここで、エラーバーの方向や終点のスタイル、値の範囲などを調整できます。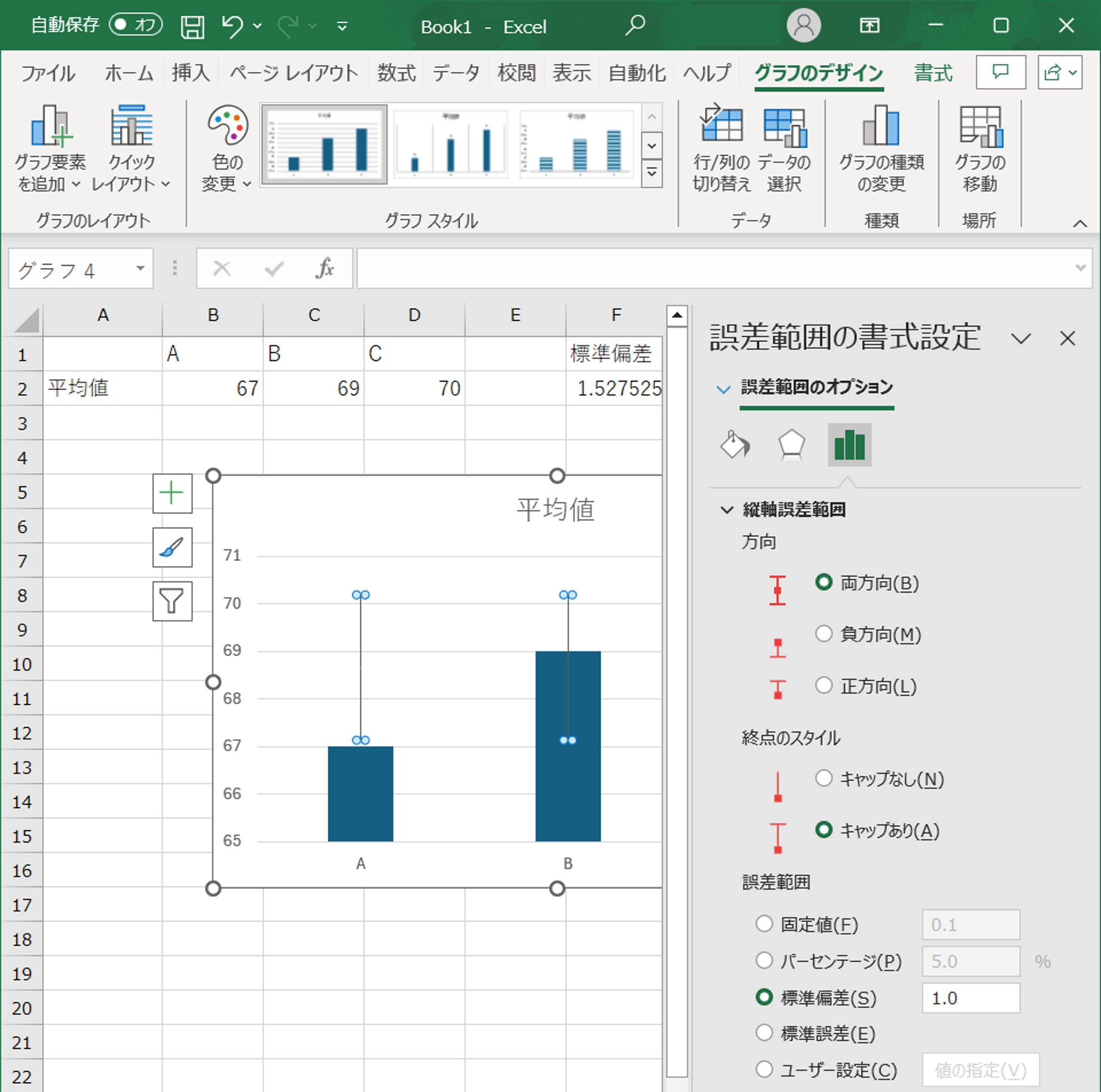
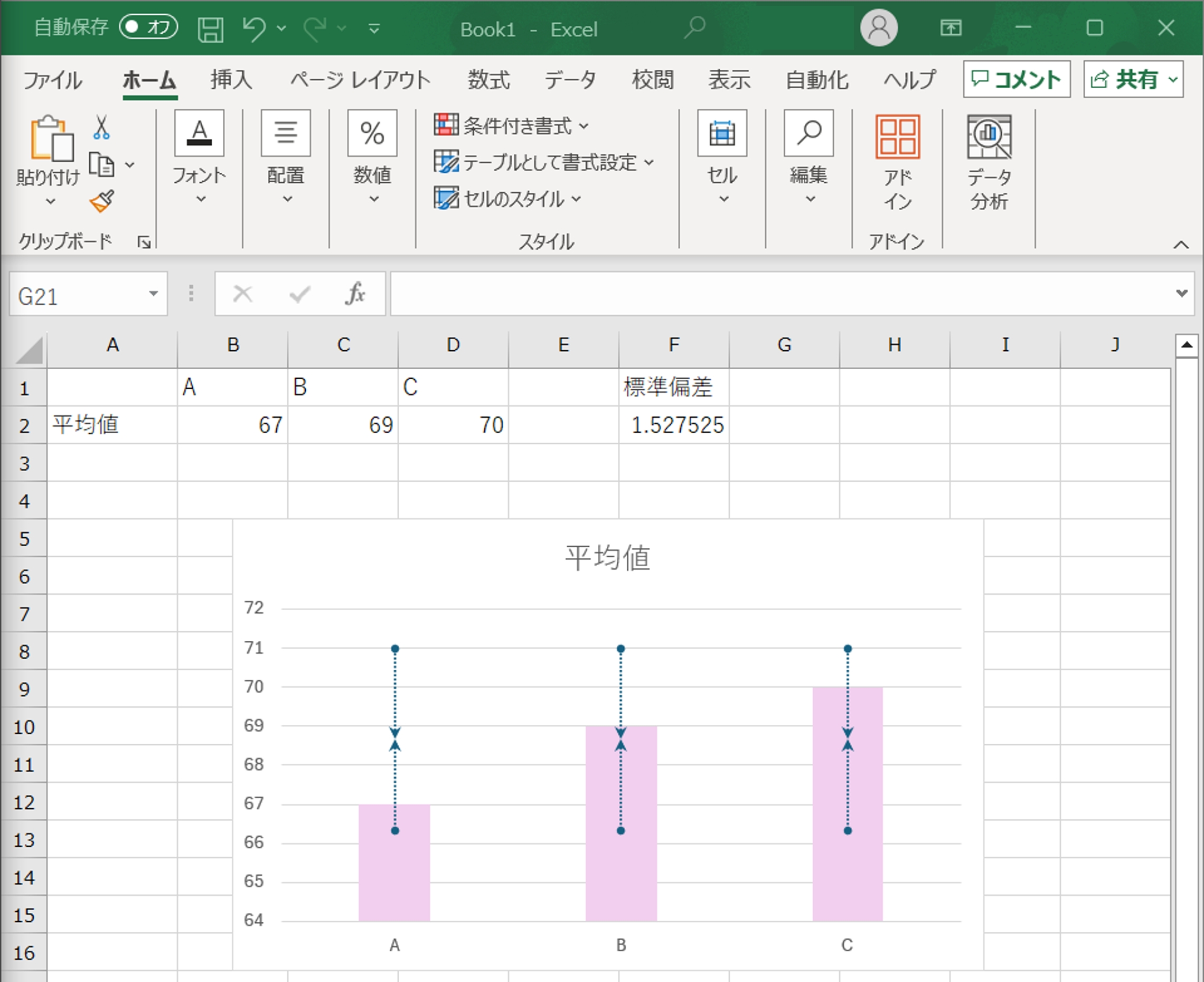
- グラフの美化:最後に、グラフのタイトルや軸ラベルを追加し、色やフォントを調整して、見やすいグラフに仕上げます。
散布図に変換する
散布図は、個々のデータポイントを視覚的に表現し、データ間の関係性や分布を見るのに適しています。特に、標準偏差を含むデータセットでは、データのばらつきや相関関係を把握するのに役立ちます。Excel(エクセル)で散布図を作成する手順は以下の通りです。
1.データの入力:散布図にするデータをExcel(エクセル)シートに入力します。通常、X軸とY軸の値をそれぞれの列に入力します。
2.グラフの作成:データ範囲を選択し、「挿入」タブをクリックします。「散布図」を選び、基本的な散布図を作成します。
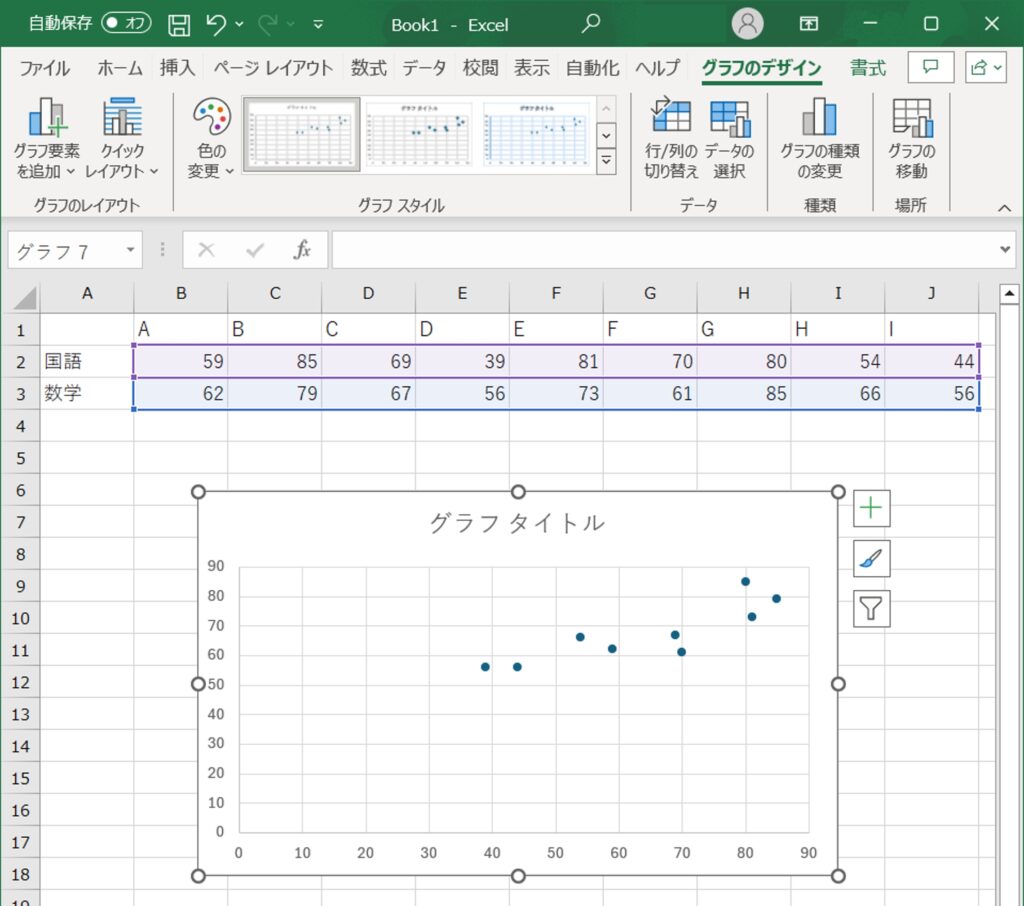
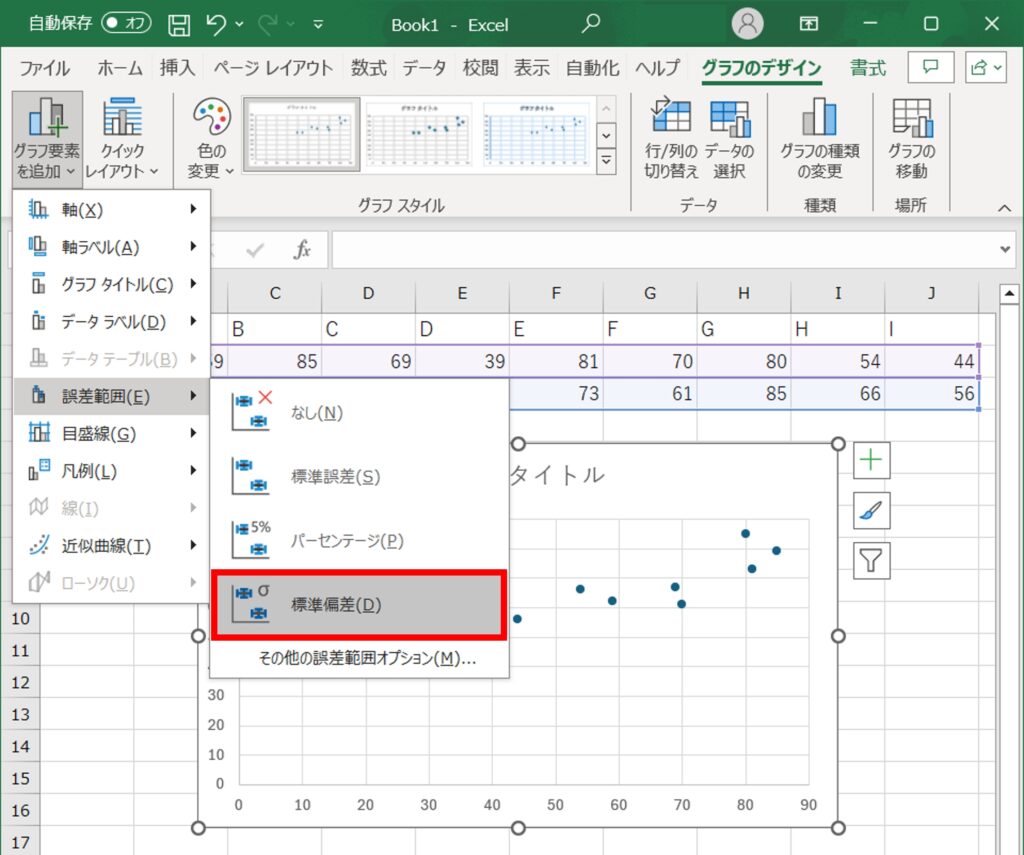
3.エラーバーの追加:散布図にもエラーバーを追加することができます。散布図をクリックし、「グラフデザイン」タブから「グラフ要素を追加」を選び、「誤差範囲」をクリックします。ここでも「標準偏差」を選択します。
4.エラーバーの編集:エラーバーの種類や表示形式をカスタマイズしたい場合、エラーバーを右クリックし、「誤差範囲の書式設定」を選びます。
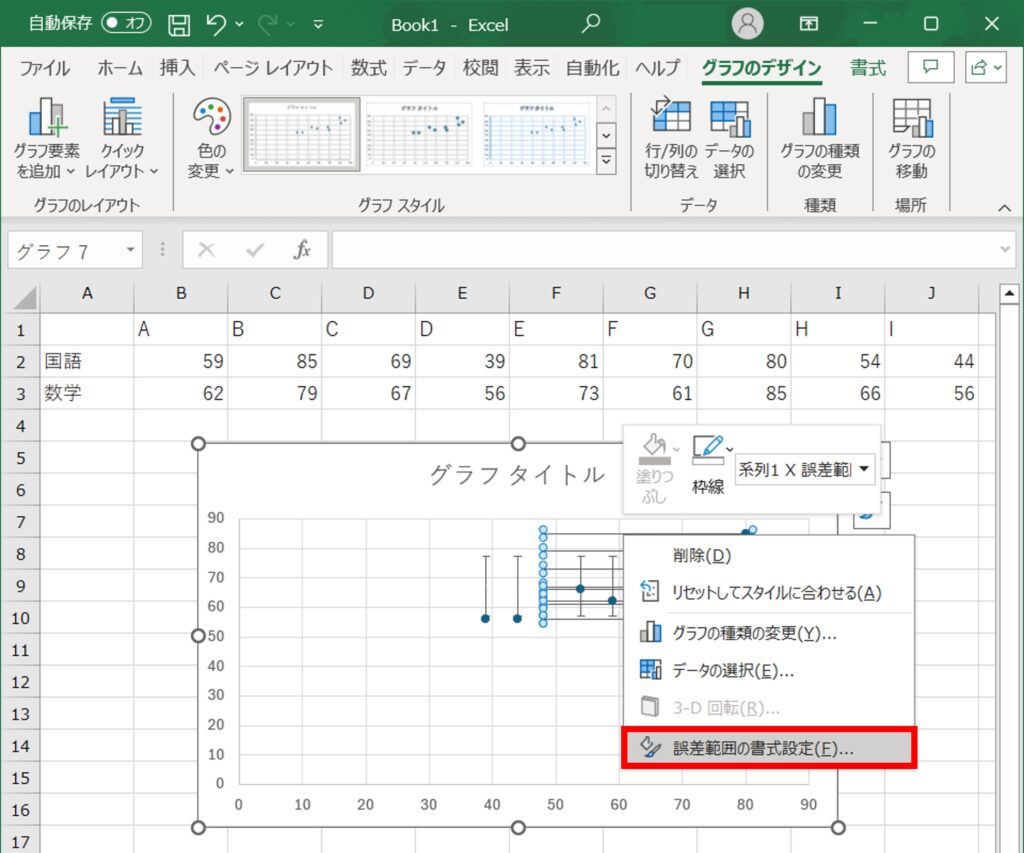
ここで、エラーバーの方向や終点のスタイル、値の範囲などを調整できます。
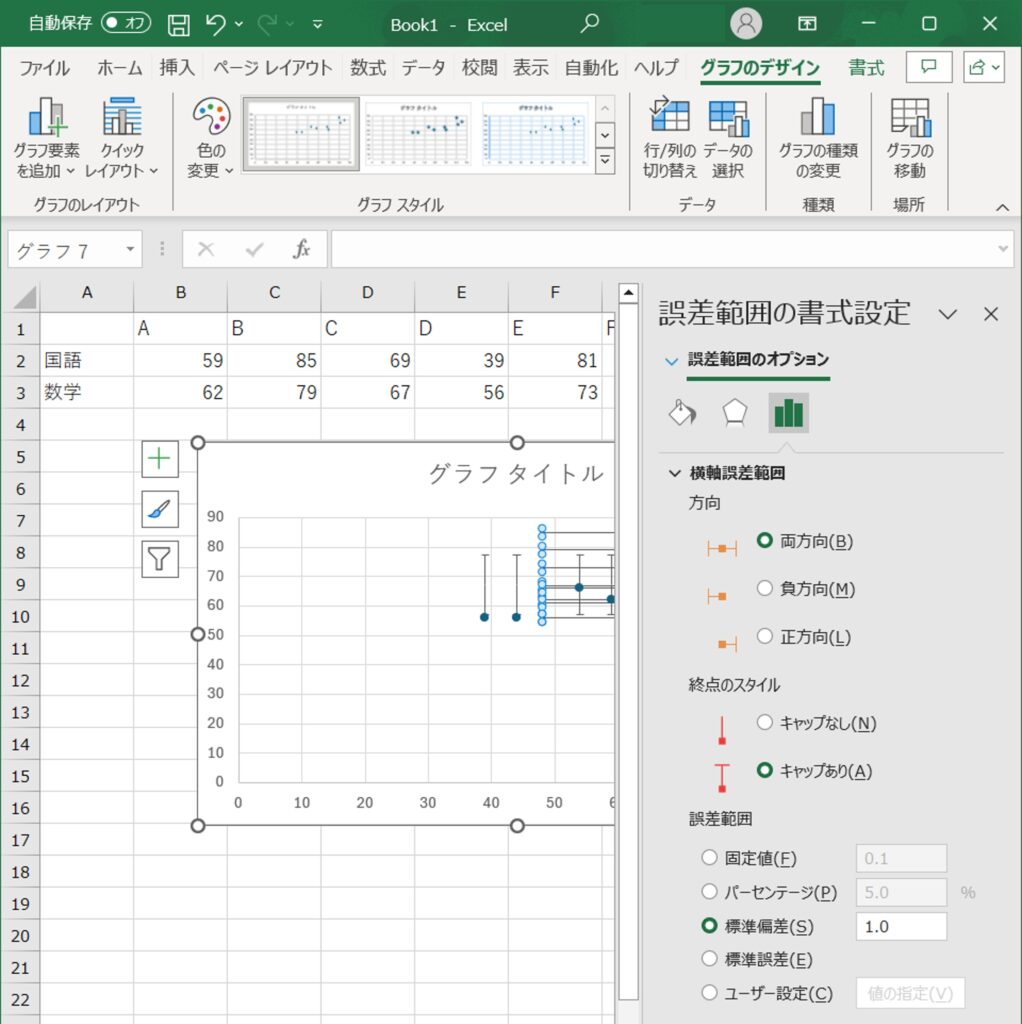
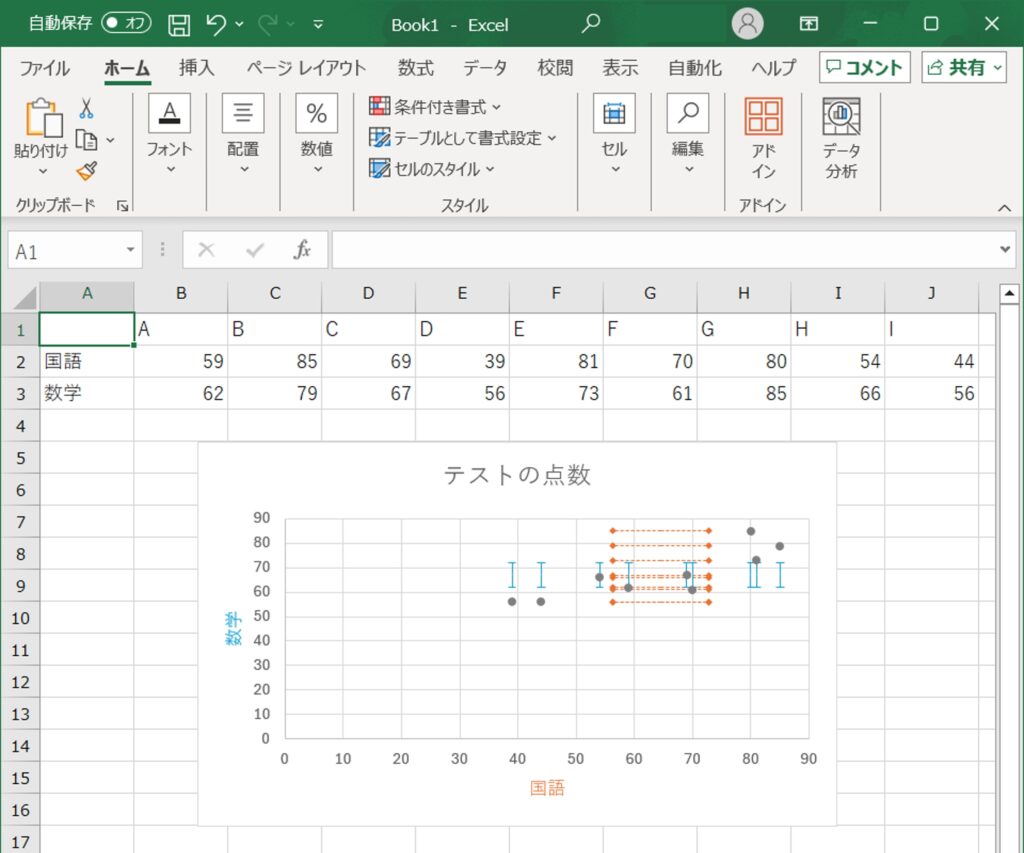
5.グラフの美化:散布図のタイトルや軸ラベルを追加し、必要に応じてデータラベルも表示させます。グリッドラインや背景色の調整も行い、視覚的にわかりやすいグラフに仕上げます。
まとめ

Excel(エクセル)で標準偏差の出し方について、関数を利用してグラフにまとめる方法を解説しました。
これらの方法を適切に使い分けることで、Excel(エクセル)を用いて効率的に標準偏差を計算し、データのばらつきを正確に把握することができます。各方法の特徴を理解し、状況に応じて最適な手法を選ぶことが重要です。これにより、データ分析の精度を高め、より信頼性の高い結果を得ることができるでしょう。